Mathcad作为一款强大的数学计算和文档工具,能够帮助用户进行复杂的数学分析。在实际应用中,验证计算结果的正确性和保留小数精度是非常重要的。本文将介绍如何在Mathcad中验证计算结果,并介绍如何控制小数的保留精度。
一、Mathcad如何验证计算结果
验证计算结果的正确性在任何工程计算中都是至关重要的,Mathcad提供了多种方法来帮助用户验证计算结果。
1. 使用单位检查
Mathcad的一大特点是它对单位的强制管理。每个变量和公式都可以附加相应的单位,这有助于自动检查计算过程中单位的一致性,避免由于单位不匹配而导致的错误。
步骤:
在变量定义时指定单位:在定义变量时,您可以直接指定单位,Mathcad会自动进行单位转换和一致性检查。
示例:
mathcad
x := 10 m // x的单位为米 v := 2 m/s // v的单位为米每秒 t := x / v // 计算时间
自动单位检查:如果公式中的单位不一致,Mathcad会提示错误,并显示单位不匹配的警告。
2. 比较不同方法的计算结果
如果您有多个计算方法,可以通过比较不同方法的计算结果来验证正确性。例如,您可以使用近似解和精确解进行对比,或者用不同的数值方法进行求解并比较结果。
步骤:
计算结果的对比:例如,您可以使用近似算法和精确解对比,或者通过改变求解参数来验证结果的稳定性。
示例:
mathcad
// 使用不同的方法计算相同的结果 result1 := (1 + sqrt(5)) / 2 // 黄金分割数 result2 := 1 + 1/sqrt(5) // 另一种近似方法 abs(result1 - result2) // 比较两者的差异
使用误差分析:您可以通过计算误差来验证结果。例如,计算精确解和近似解之间的差异,并检查差异是否在可接受的误差范围内。
3. 确保数值稳定性
在进行复杂计算时,确保数值稳定性是非常重要的。Mathcad提供了数值求解和符号求解的功能,用户可以选择合适的计算方法,避免由于数值不稳定而导致的计算误差。
符号计算:对于需要高精度的计算,Mathcad支持符号计算,这样可以避免由于数值计算引入的误差。
示例:
mathcad
x := sqrt(2) // 符号计算,可以保留精确解
数值计算:对于大多数工程应用,Mathcad的数值计算已经足够精确,但在计算时可以注意设置合适的精度。
4. 交叉验证与第三方工具
对于一些复杂的计算,可以通过与其他工具进行交叉验证。例如,您可以将Mathcad的计算结果与Excel、Matlab等工具进行对比,或者通过手动推导公式的方式进行检查。
交叉验证:将Mathcad的结果与其他已知计算结果进行对比,检查两者的一致性。
示例:
mathcad
// 比较Mathcad结果与手工计算结果 resultMathcad := 3 * pi^2 + 4 // Mathcad计算的结果 resultManual := 3 * 9.8696 + 4 // 手工计算的结果 abs(resultMathcad - resultManual) // 检查误差
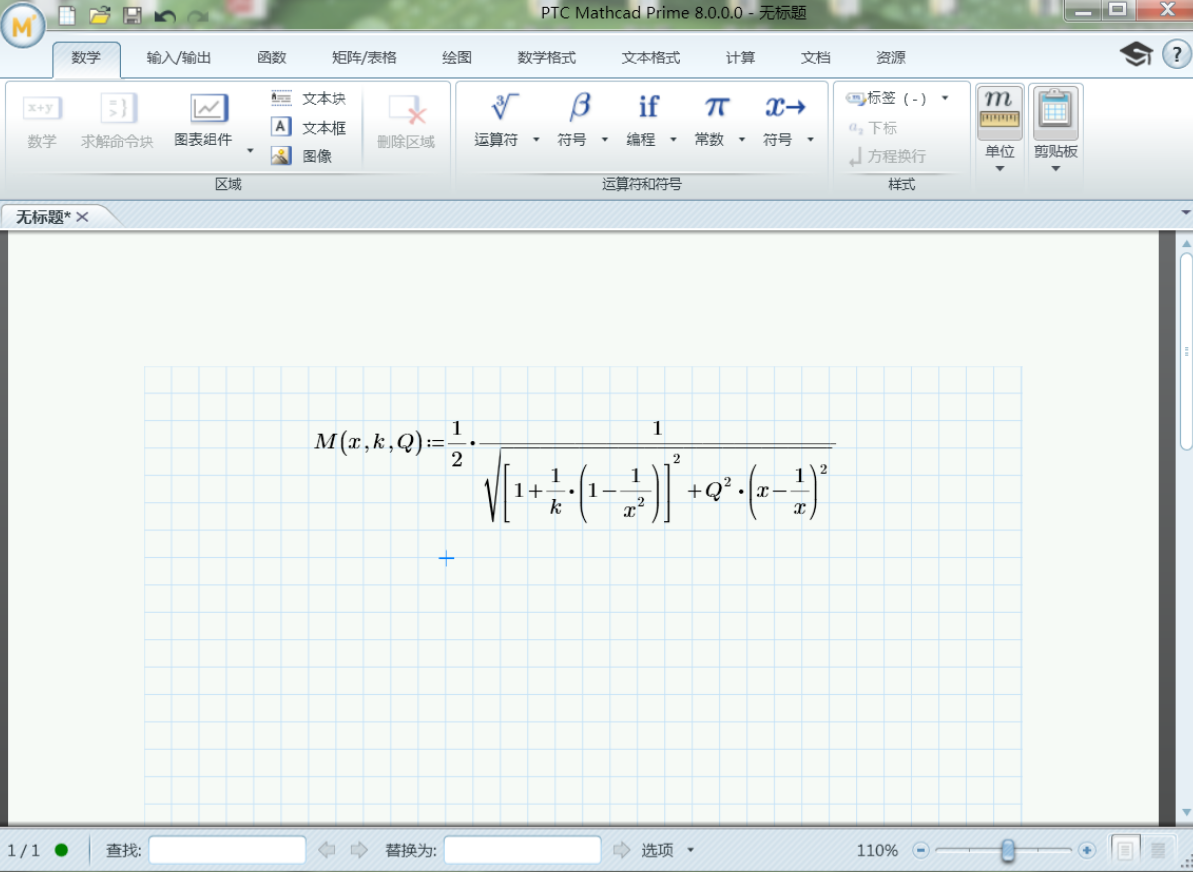
二、Mathcad怎么保留小数
在实际的计算中,Mathcad的默认设置是自动根据需要显示小数位数,但有时为了更高的精度或统一格式,我们可能需要调整小数的显示格式。Mathcad允许用户通过设置显示格式来控制结果的小数精度。
1. 设置小数显示精度
Mathcad提供了设置小数精度的功能,您可以选择显示结果的小数位数。通常,这可以通过格式设置来调整。
步骤:
调整数字精度:
选中公式的结果区域,右键点击并选择“数字格式”。
在弹出的对话框中,选择“数字精度”或“小数位数”,然后设置所需的小数位数。
示例:
设置为保留3位小数:
mathcad
x := 3.14159 x // 显示结果为 3.142
2. 使用fix()函数控制小数位数
Mathcad中的fix()函数可以帮助您控制数字的小数位数。如果您希望显示的结果精确到特定的小数位数,可以使用该函数。
步骤:
使用fix()函数:将数字传递给fix()函数,指定保留的小数位数。
示例:
mathcad
x := 3.14159265358979 fix(x, 3) // 保留三位小数,结果为3.142
3. 控制整个文档的小数精度
如果您希望整个文档中所有结果都显示为统一的小数位数,可以设置文档的默认显示精度。通过修改文档设置,Mathcad将自动格式化所有数字。
步骤:
设置文档默认小数精度:
在“选项”中,您可以设置默认的小数位数。例如,设置显示所有数字保留两位小数。
4. 使用round()函数进行四舍五入
如果需要将结果四舍五入到某个特定的小数位,可以使用round()函数。它允许您指定保留的小数位数,并且自动进行四舍五入。
示例:
mathcad
x := 3.14159265358979 round(x, 2) // 结果为3.14
三、如何进行计算结果的误差分析与精度控制
在工程计算中,误差分析和精度控制是非常重要的。尤其是在处理数值计算时,数值误差可能会影响最终结果的准确性。在Mathcad中,您可以通过以下方法对计算结果进行误差分析:
1. 相对误差和绝对误差
为了评估计算结果的误差,您可以计算相对误差和绝对误差,并根据误差范围判断结果的精度是否符合要求。
相对误差:
RelativeError=∣xtrue−xapprox∣∣xtrue∣\text{Relative Error} = \frac{|x_{true} - x_{approx}|}{|x_{true}|}RelativeError=∣xtrue ∣∣xtrue −xapprox ∣
绝对误差:
AbsoluteError=∣xtrue−xapprox∣\text{Absolute Error} = |x_{true} - x_{approx}|AbsoluteError=∣xtrue −xapprox ∣
2. 自定义精度控制
根据实际需求,您可以通过数值求解时的精度控制(如调整Tolerance、MaxIter等参数)来获得更精确的结果。
示例:
mathcad
x := 3.14159 tolerance := 1e-5 if abs(x - 3.14) < tolerance then "Acceptable" else "Not Acceptable"
3. 采用符号计算提高精度
对于一些数学计算,Mathcad支持符号计算,这能够避免数值误差的问题。使用符号计算可以确保计算结果的精确性。
示例:
mathcad
x := sqrt(2) // 符号计算,结果为 sqrt(2)

总结
在Mathcad中,验证计算结果和控制小数精度是确保计算准确性和可读性的关键。通过合理使用单位检查、交叉验证、误差分析等方法,您可以有效地验证计算结果的正确性;而通过调整数字格式、使用fix()、round()等函数,您可以灵活地控制小数精度,满足不同计算要求。此外,结合符号计算和数值精度控制,Mathcad能够帮助您实现更精确和稳定的计算。

