在本文中，我将仅从载荷条件开始并使用积分，推导均匀载荷、简支梁的剪力、弯矩、斜率和挠度函数。然后对三角载荷重复该过程。

在积分时，Mathcad 不包括积分常数 C。这需要使用已知约束来解决。

由于均匀载荷向下作用，我将使用 w（力/长度）的负值。

我还将使用一些数值数据来验证计算出的函数：

• 梁长：长度=20 英尺
•  
• 均匀载荷：W=2.0 千磅/英尺
•  
• 弹性模量：E1=29000 ksi
•  
• 转动惯量：I1= 448in4

均匀加载

加载中

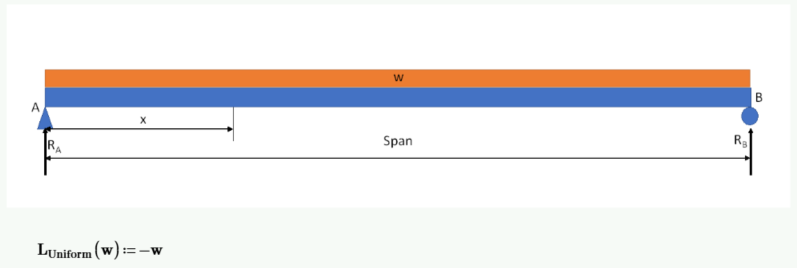
通过对点 B 处的力矩求和来计算左反应。

剪切

通过积分载荷函数并包括积分常数 C1 来计算剪切函数。

解出积分常数 C1。我们知道，在 x=0 时，剪切力等于左侧反作用力 R A。

C1 等于 Span*w/2。现在可以将其输入到剪切函数中，并且可以重新定义剪切函数，而不需要将 C1 作为输入变量。

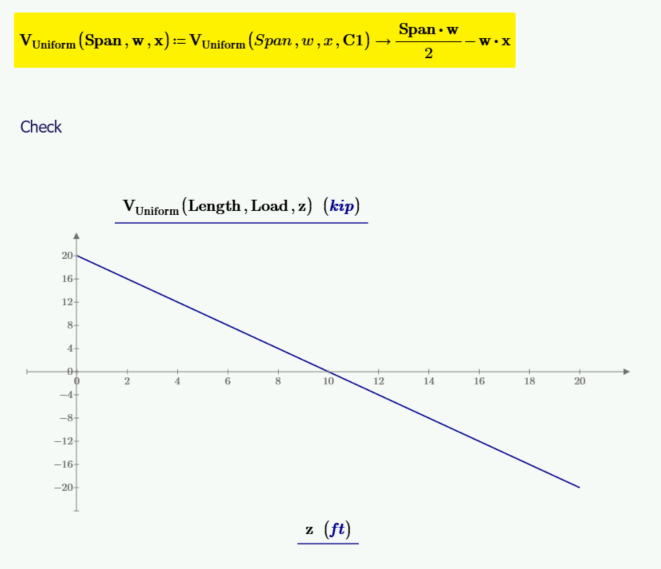
片刻

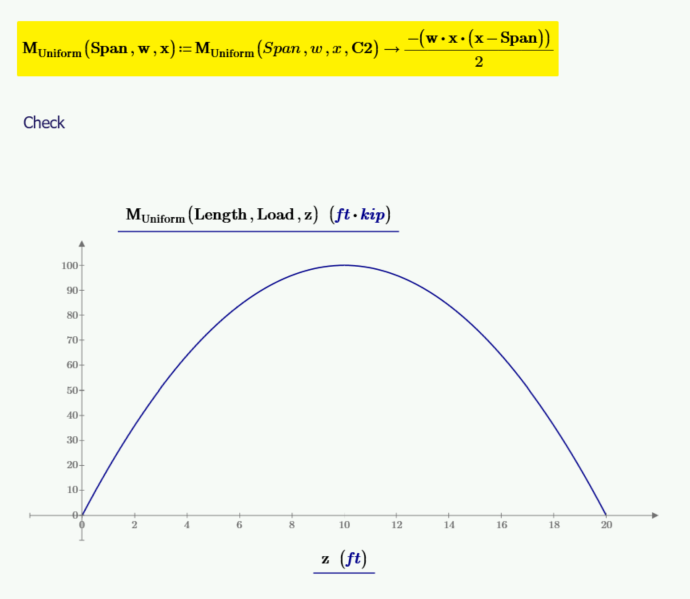
通过积分剪切函数并包含积分常数 C2 来计算力矩函数。

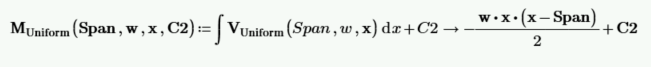
求积分常数 C2。我们知道，在 x=0 时，矩为 0。

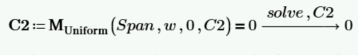
C2 等于 0，现在可以将其输入到矩函数中，并且可以重新定义矩函数，而不需要 C2 作为输入变量。

坡

根据材料力学，梁的曲率半径 p 的关系定义为 1/p = M/(E*I)，力矩与斜率θ的关系定义为 M = E * I * d/dx( θ)。通过积分 M/(E*I) 来计算斜率。

有两种方法可以求解均匀载荷梁的 C3。

首先，我们知道对于均匀受力的梁，在最大弯矩点处梁的斜率为零，并且我们知道最大弯矩发生在剪力为零的位置。求解 C3 的第一种方法是计算零剪力的位置，并在零剪力的位置使用斜率=0 的约束。  

计算 C3 的第二种方法是等到挠度函数导出后，使用挠度等于零的两个位置。然后使用两个方程求解两个未知数 C3 和 C4。

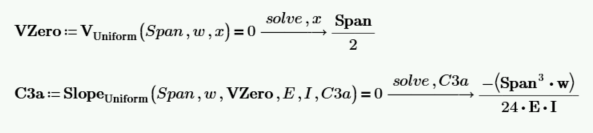
偏转

通过积分斜率函数来计算挠度。请注意，必须求解两个积分常数。

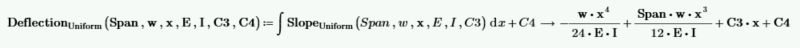
C3 和 C4 未知。x=0 处的挠度为 0，x=Span 处的挠度为 0。使用这两个值来求解 C3 和 C4。

C3 等于 -((span 3 * w) / (24 * E * I))。现在可以将其输入到斜率函数中，并且可以重新定义斜率函数，而无需将 C3 作为输入变量。C4 等于零，因此可以消除 C4。

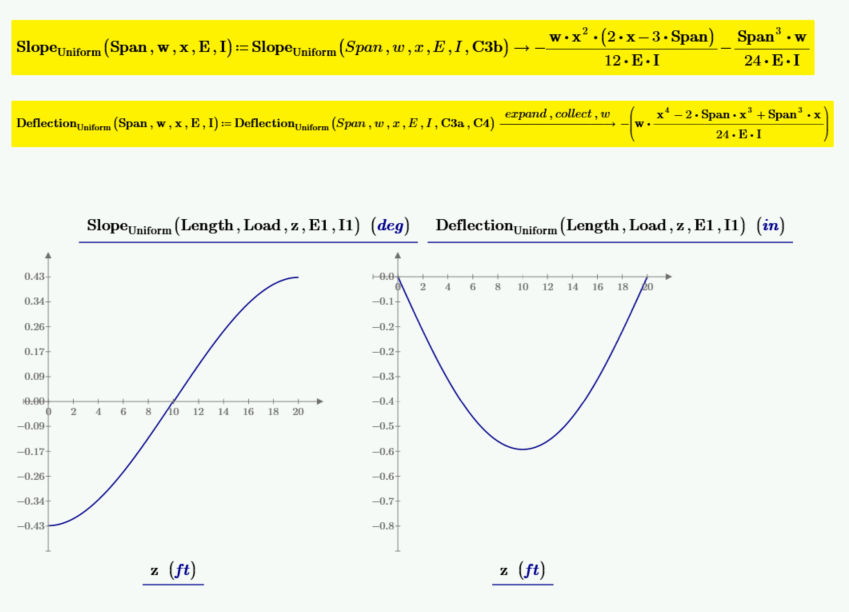
下图为剪力、力矩、梁斜率和挠度的图。斜率和挠度的值乘以 100，以便按所需比例绘制。位于跨度中间的垂直标记位于剪力为零、力矩最大、斜率为零和挠度最大的位置。

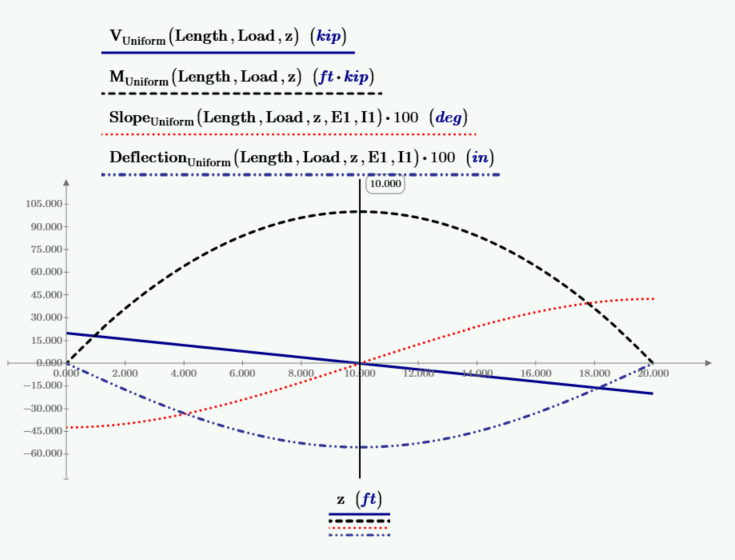
推导一个函数来计算均匀载荷梁的最大挠度。最大挠度发生在梁斜率为 0、弯矩最大且剪力为 0 的地方。此值 VZero 是先前计算的。

三角载荷

下面的示例重复了上面用于推导计算三角形载荷梁的剪力、弯矩、斜率和挠度的函数的过程，从三角形载荷函数开始。

加载中

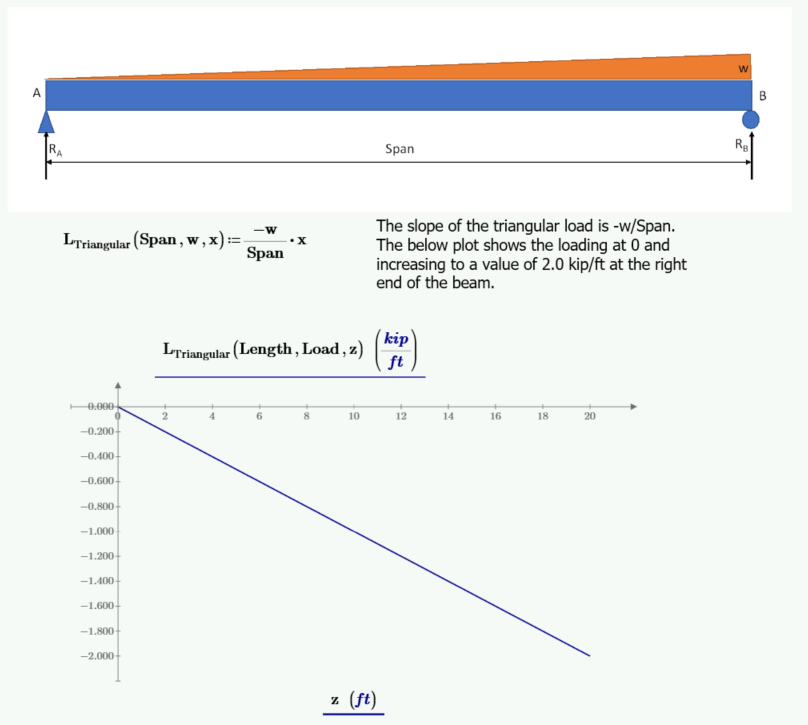
通过对点 B 处的力矩求和来计算左反应。

剪切

通过积分载荷函数并包括积分常数 CT1 来计算剪切函数。

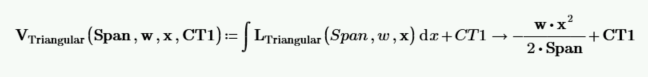
解出积分常数 CT1。我们知道，在 x=0 时，剪切力等于左侧反作用力 R A。

CT1 等于 Span*w/6。现在可以将其输入到剪切函数中，并且可以重新定义剪切函数，而无需将 CT1 作为输入变量。

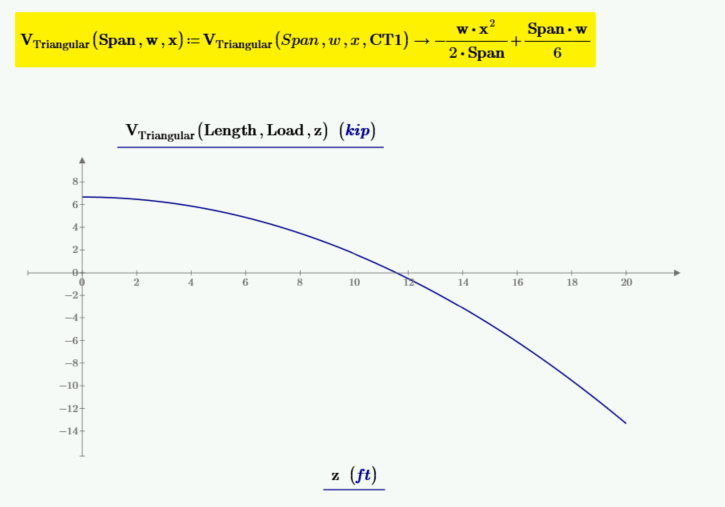
片刻

通过积分剪切函数并包括积分常数 CT2 来计算力矩函数。

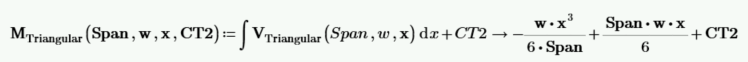
解出积分常数 CT2。x=0 时的矩为 0。

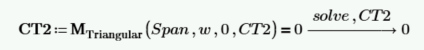
CT2 等于 0，现在可以将其输入到矩函数中，并且可以重新定义矩函数，而不需要 CT2 作为输入变量。

坡

根据材料力学，梁的曲率半径 p 的关系定义为 1/p = M/E * I，力矩与斜率 θ 的关系定义为 M = E * I * d/dx(θ)。通过积分 M/E * I 来计算斜率。

对于三角形载荷的情况，最大挠度不会发生在零剪切和最大弯矩的位置。因此，我们不知道解决 CT3 的任何约束。  

对于这种情况，求解 CT3 的唯一方法是等到偏转函数导出，然后使用偏转等于零的两个位置来求解两个未知数 CT3 和 CT4。

偏转

通过积分斜率函数来计算挠度。请注意，必须求解两个积分常数。

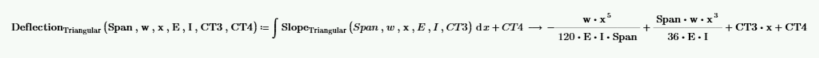
CT3 和 CT4 未知。x=0 处的挠度为 0，x=Span 处的挠度为 0。使用这两个值来求解 CT3 和 CT4。

既然已知 CT3 和 CT4，就可以重新定义斜率和挠度的函数。

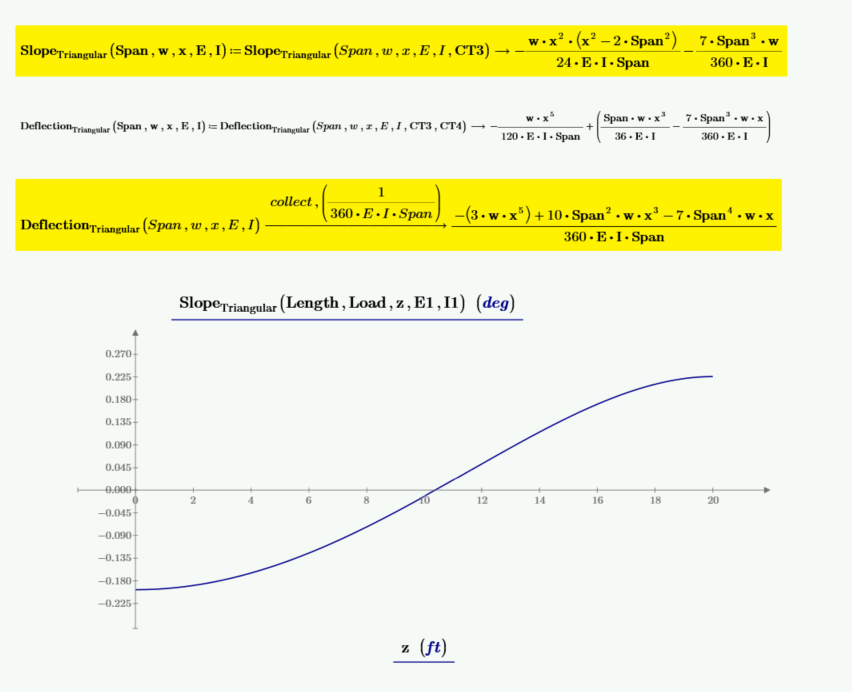
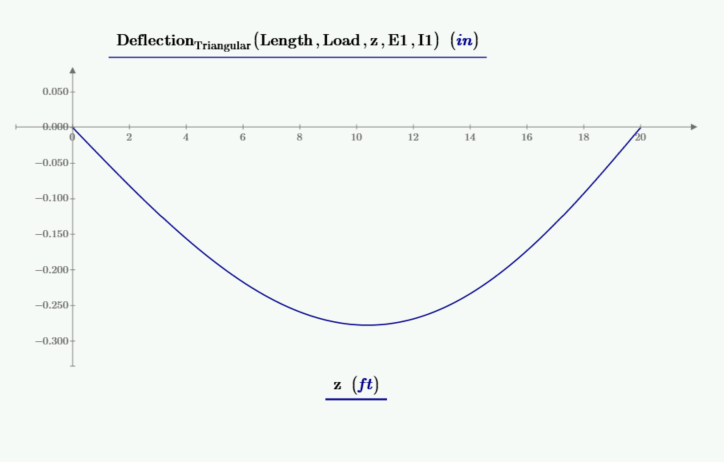
推导一个函数来计算三角形载荷的最大挠度，该载荷发生在梁斜率等于零的地方。x 的解有四个解。

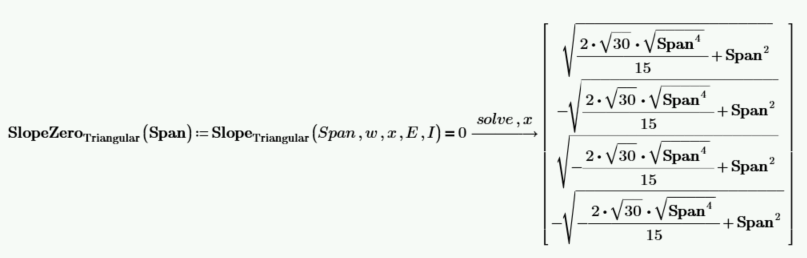
检查数值结果并选择第三个解决方案作为零梁斜率的位置。注意：下标 3 是使用左括号 [ 获得的。

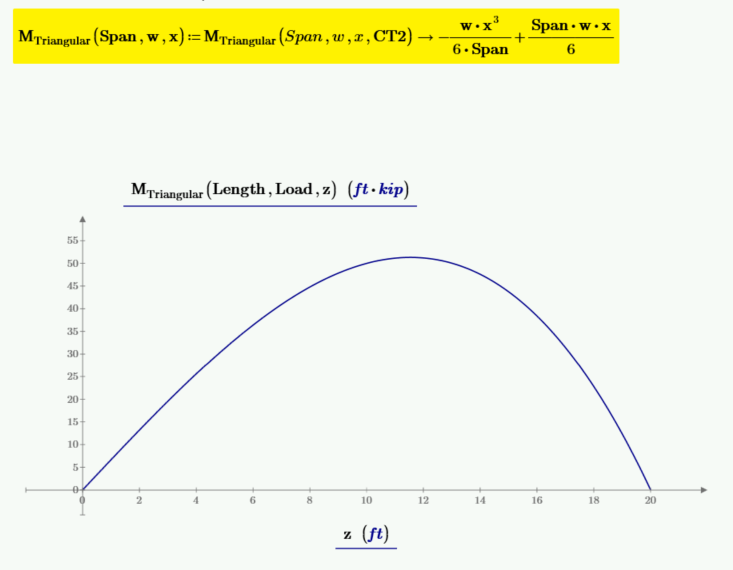
下图是剪力、力矩、梁斜率和挠度的图。斜率和挠度的值乘以 100，以便按所需比例绘制。左侧垂直标记位于零梁斜率的位置和最大挠度的位置。右侧垂直标记位于零剪力和最大力矩的位置。

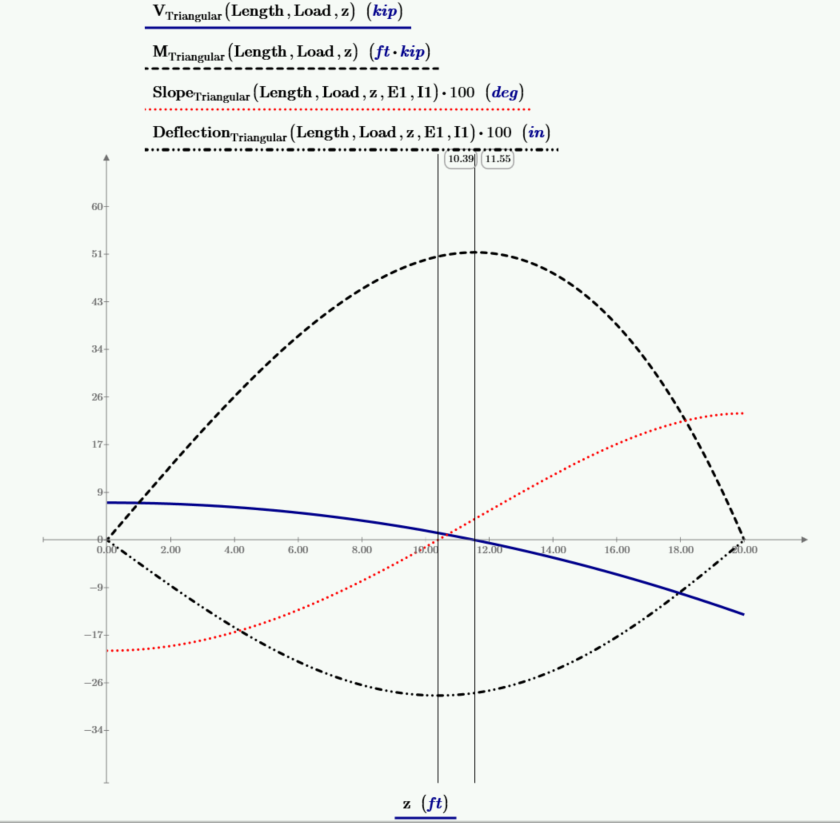
在本文中，我使用积分法从载荷函数开始推导出挠度函数。在此过程中，我推导出了剪力、弯矩和梁斜率函数。这些函数是使用 AISC钢结构手册中的已知方程检查的。

积分是 Mathcad 工具箱中的一个强大工具。我演示了如何使用已知约束求解积分常数，以及如何将求解关键字与符号求值运算符以及其他关键字结合使用，以帮助导出所需的函数。

在本文中，我使用了梁上的载荷来说明这些概念，但这些相同的概念可以用于许多其他科学和工程领域。本文的示例说明了以下内容的用法：

• 功能
•  
• 通过符号求值导出函数，尤其是在数值未知的情况下
•  
• 具有多条轨迹的 XY 图
•  
• 垂直标记用于说明地块上的位置
•  
• 范围变量
•  
• 积分并求解积分常数